Signos del álgebra: Existen tres tipos:
1. Signos de operación:
Las mismas operaciones que se usan en aritmética, se verifican con cantidades también en álgebra. Estas son por ejemplo: suma, resta, multiplicación, división, extracción de raíces y elevación a potencias, los cuales son indicados a través de los siguientes signos:
⦁ + (más) es el signo de la suma; por lo tanto a + b se leé 'a más b'.
⦁ - (menos) es el signo de la resta; por lo tanto a - b se leé 'a menos b'.
⦁ x (por) es el signo de la multiplicación; por lo tanto a x b se leé 'a por b'.
⦁ - (menos) es el signo de la resta; por lo tanto a - b se leé 'a menos b'.
En algunas ocasiones solemos usar los siguientes signos para representar la multiplicación (. 'un punto' ó * 'un asterisco'). Cuando usamos el punto, seria lógico colocar los factores entre paréntesis (a).(b). También es permitido omitir el signo de multiplicación entre factores literales o numéricos, veamos algunos ejemplos a continuación:
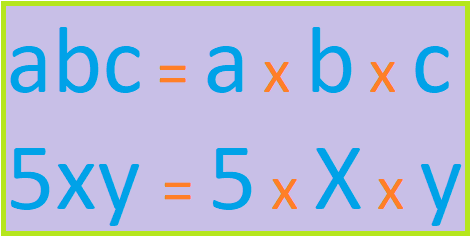
⦁ ÷ (entre) es el signo de la división; por lo tanto a ÷ b se lee 'a entre b'. En muchos casos también solemos usar otros signos para representar la división, veamos los ejemplos a continuación:
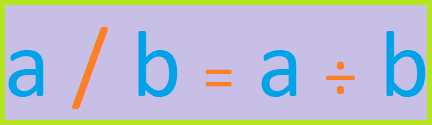
⦁ X2 (exponente), es el signo de la elevación a potencia. Es un número pequeño que se coloca en la parte de arriba a la derecha de una cantidad, ‘a dicha cantidad se le llama base’, Este signo indica las veces que la base será tomada como factor. Por ejemplo:
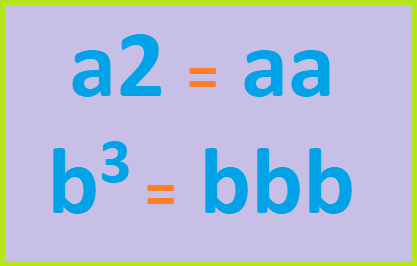
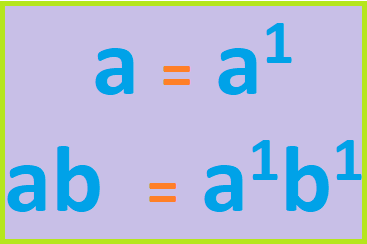
⦁ √ (raíz), se le llama signo radical, y debajo de dicho signo se tiende a colocar la cantidad a la que se le extraerá la raíz. De tal forma que: √a, representa la raíz cuadrada de a, es decir que la cantidad que se eleva al cuadrado, reproduce la cantidad a; de igual manera; 3√b, representa la raíz cúbica de b, es decir que la cantidad que se eleva al cubo, reproduce la cantidad b.
2. Signos de relación:
Son los signos que se usan para indicar la relación existente entre 2 cantidades, por ejemplo:
⦁ = (igual a), por lo tanto a = b se lee ‘a igual a b’.
⦁ > (mayor que), por lo tanto a + b > c se lee ‘a + b mayor que m’.
⦁ < (menor que), por lo tanto a < b + c se lee ‘a menor que b + c.
3. Signos de agrupación:
Son los signos que indican que la operación que se encuentra dentro de ellos debe ser la primera en efectuarse, los signos son los siguientes:
⦁ Paréntesis ordinario ( )
⦁ Paréntesis angular o corchete [ ]
⦁ Llaves { }
⦁ Barra vínculo -
Coeficiente:
Se le llama coeficiente a uno de los factores en un producto de 2 factores. Por ejemplo:
⦁ Se presenta el producto 2a, donde el 2 viene a ser el coeficiente de a, indicando que el factor a, es tomado como sumando 2 veces, es decir:
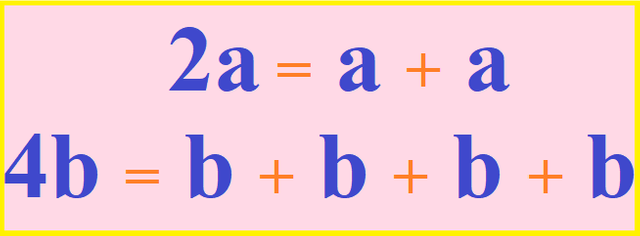
⦁ Se presenta el coeficiente ab, donde a viene a ser el coeficiente de b, indicando que el factor b, es tomado como sumando a veces, es decir:
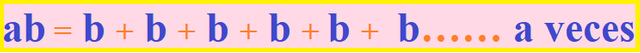
Cuando existe un producto de mas de 2 factores, en este caso uno o mas de ellos representan los coeficientes de los factores restantes. Por ejemplo:
En caso de que alguna cantidad no tenga un coeficiente numérico, entonces su coeficiente sería la unidad, por ejemplo:
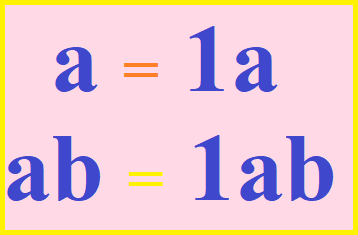
Modo de resolver los problemas en aritmética y en álgebra:
Veremos a continuación un ejemplo que nos va a a mostrar la diferencia entre el método algebraico (este fundado en la notación algebraica y en la generalización que implica) y el método aritmético.
Las edades de m y n suman 48 años. Si la edad de n es 5 veces la edad de m, ¿Qué edad tiene cada uno?
1. Método aritmético:

2. Método algebraico:

Cantidades positivas y negativas:
En álgebra, al estudiarse cantidades que se toman en sentidos opuestos, se expresa la condición (valor relativo) de la cantidad a través de los signos + y -, se antepone el signo + a las cantidades que son tomadas en sentido determinado (cantidades positivas) y se antepone el signo - a las cantidades que se toman en sentido opuesto a las positivas, (cantidades negativas).
De esta manera el haber es designado con el signo + y las deudas con el signo -. Quiere decir que para expresar que alguien tiene 50 bs de haber, se dice que tiene +50 bs, en caso de ser una deuda, se expresa -50 bs.
En un termómetro también designamos los grados sobre 0 con el signo + y los grados bajo cero con el signo -. De esta manera si queremos indicar que el termómetro marca 5º sobre cero, se expresa +5º, y para indicar el caso contrario (5º bajo creo), se expresa -5º.
El camino que se recorre a la derecha o hacía arriba de un punto se designa con el signo +, y el camino que se recorre hacía la izquierda o hacia abajo se designa con el signo -. De esta manera si recorremos 100 m. a la derecha de un punto dado, se expresa +100 m., y si lo hacemos hacía la izquierda, se expresa -100 m.
También en el cristianismo encontramos que el tiempo transcurrido después de Cristo, se designa con el signo + y el tiempo antes de Cristo, se designa con el signo -. Por ejemplo +50 años significa que son 50 años después de Cristo y -50 años significa 50 años antes de Cristo.
También lo podemos expresar al enterrar un poste en el suelo, la parte del poste que se encuentra del suelo hacía arriba, lo que es visible, se representa con el signo + y lo que no podemos ver porque queda del piso hacía abajo se representa con el signo -. Quiere decir que para expresar la longitud del poste que se encuentra del suelo hacía arriba, sería +10 m. y la parte que queda debajo del suelo es de -7 m.
Por otro lado podemos designar con el signo + la latitud norte y la longitud este, de manera que la latitud sur y longitud oeste se expresan con el -. Quiere decir que si un punto de la tierra cuya situación geográfica es: +45º de longitud y -15º de latitud, se encontrará a 45º al este del primer meridiano y a -15º bajo el ecuador.
Elección del sentido positivo:
Para fijar el sentido positivo en cantidades que se pueden tomar en 2 sentidos opuestos es arbitraria, depende de lo que queremos; es decir, podemos tomar como sentido positivo lo que se nos ocurra, lo que si debe quedar claro es que lo contrario a lo que tomamos, será el sentido negativo.
Quiere decir que si tomamos como mencionábamos en los párrafos anteriores, el recorrido a la derecha como sentido positivo, de forma automática el camino a la izquierda será el negativo, pero bien podríamos tomar el camino a la izquierda como el positivo y el de la derecha negativo, eso de acuerdo al criterio de cada quien.
Por ejemplo, si de un segmento de m a n, tomamos como sentido positivo el sentido de m a n, entonces el sentido de n hacía m sería negativo
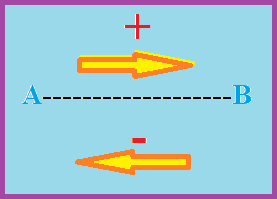
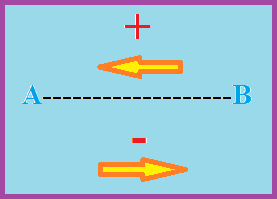
Cero:
Es la ausencia de cantidad. Quiere decir que cuando representamos el estado económico de una empresa por 0, quiere decir que no tiene haber ni deuda.
Las cantidades positivas son mayores que 0 y las negativas menores que 0. Es decir +2 es una cantidad que es 2 unidades mayor a 0; +4 es una cantidad 4 unidades mayor a 0, mientras que -3 es una cantidad 3 unidades menor a 0.
En 2 cantidades positivas, es mayor la de mayor valor absoluto, por ejemplo: +4 es mayor que +2, pero en caso de ser cantidades negativas, es mayor la cantidad de menor valor absoluto, por ejemplo: -2 es mayor que -6.